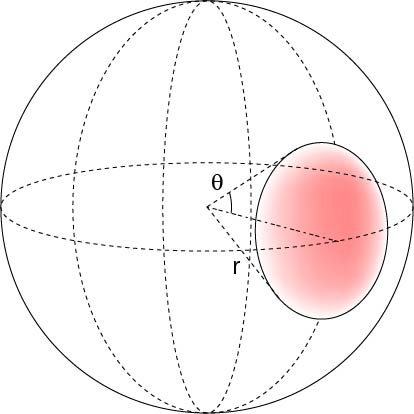
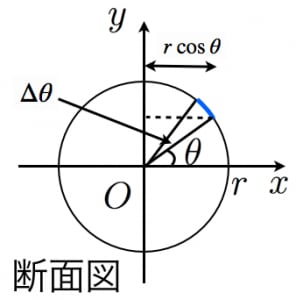
球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。面積を求める例題 まずは面積を求める例題から説明します。面積を求めるときのポイントは どのような線が集まって面を形成しているか をイメージすることが大切です。 三角形 下の図のように\(y=x\)の直線があり、原点,\((1,0)\),\((1,1)\)の3点を結ぶ三角形の面積\(S\)を求めてみたいと思います。最後に 球体の表面積 球体の表面積 目標:積分を用いて上式を導出する 方法を2つ考えました. 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える.
学校で球の面積の求め方を 3分の2すると言われたのですが 調べ Yahoo 知恵袋
球体 の 面積 の 求め 方 なぜ 4
球体 の 面積 の 求め 方 なぜ 4-円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径
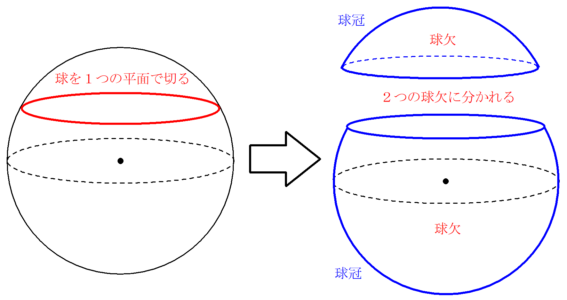


球欠と球冠 Fukusukeの数学めも
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事容積とは?1分でわかる意味、求め方、単位、円柱の容積、体積との違い 円の断面積は?1分でわかる意味、公式、計算方法と求め方、直径との関係 まとめ 今回は、円柱の容積について説明しました。求め方と式など理解頂けたと思います。球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
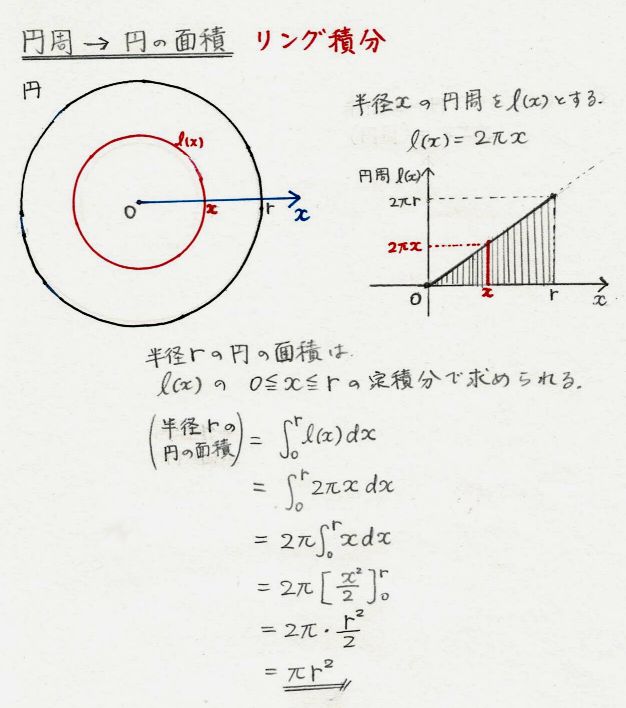
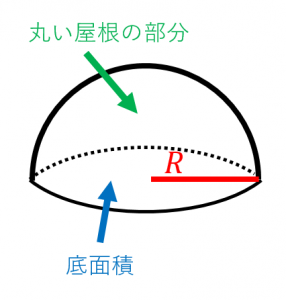
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして球の表面積を求める公式は、S = 4πr^2 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。半球の体積の求め方 半球の体積の求め方は簡単です。 球体の体積に×2分の1 をすればいいだけです。 V=4/3πr3×1/2 これに代入すれば、半球の体積は求められます。 複数の円が重なった部分の面積の求め方
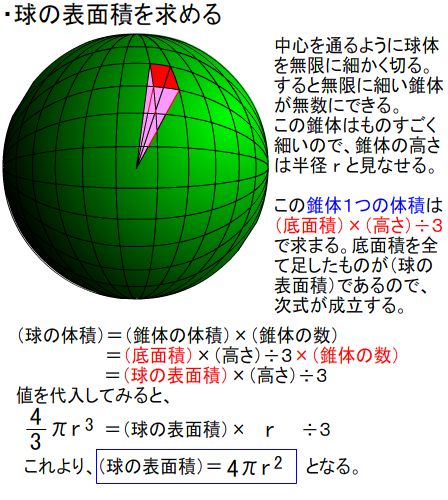
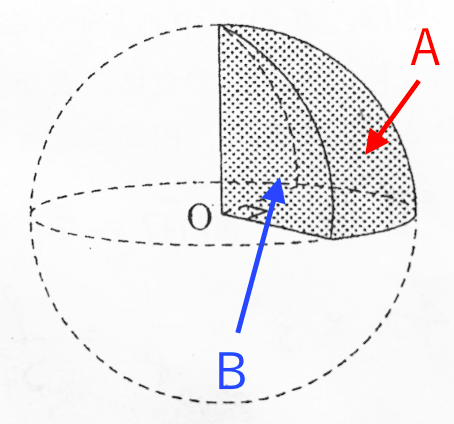
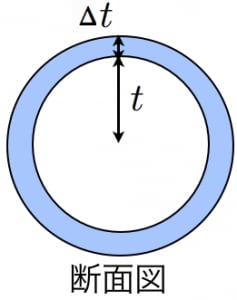
方法③:球体を細かく切る 指針(考え方) 球体を切って細かくする→表面積を考える 細かく切る 球体の表面に薄いマクがはってあることをイメージする マクの面積=球の表面積 球体を図のように切る. これを6回繰り返す. 立方体のような物体1つと円形度 circularity (等面積円の円周)/(周長) 球の表面積 \(\pi D^2\) 球の体積 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3\) 球の質量 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3 \rho\) 球の体積基準比表面積(単位体積当たりの表面積)(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして



球体の表面積 積分で求める方法 うちーノート



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
②球の表面積の公式の求め方(1) 次に、球の表面積の公式の求め方について考察する。 まずは体積のときと同様にすると、図1において、 球の中心から距離 x の点で切った断面である円の 円周の長さは、L(x)=2π√(r 2 -x 2) となる。 よって、球の表面積Sは数学 何度もすみません。 今度は「球体の面積の求め方」を知りたくなりました。 (学校で使うので) 誰でも良いので、よろしくお願いします。球の表面積の求め方公式 半径 の球の表面積を とすると、球の表面積 は次の公式で求められます。 (例題)半径が4cmの球の表面積を求めましょう。 求める球の表面積を 、半径を とすると、 より 答え cm² スポンサードリンク



球の表面積の求め方 公式と計算例



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
優雅 球体 表面積 求め 方 球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説し 中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学び数学 何度もすみません。 今度は「球体の面積の求め方」を知りたくなりました。 (学校で使うので) 誰でも良いので、よろしくお願いします。球の表面積の求め方公式 半径 の球の表面積を とすると、球の表面積 は次の公式で求められます。 (例題)半径が4cmの球の表面積を求めましょう。 求める球の表面積を 、半径を とすると、 より 答え cm² スポンサードリンク


用語与太話 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ



球の体積 球の表面積の公式の導出 積分 優技録
最新球体 の 表面積 の 求め 方 正四面体とは 体積 表面積の公式や高さ 重心の求め方 展開図の 球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus 正八面体の体積 表面積 外接球の半径 内接球の半径 具体例で学ぶ数学面積を求める例題 まずは面積を求める例題から説明します。面積を求めるときのポイントは どのような線が集まって面を形成しているか をイメージすることが大切です。 三角形 下の図のように\(y=x\)の直線があり、原点,\((1,0)\),\((1,1)\)の3点を結ぶ三角形の面積\(S\)を求めてみたいと思います。☝️ 面積なので単位は\(cm^2\)です! 球の体積の求め方! \(V=\frac{4πr^3}{3}\) (球の体積をV、半径r、円周率π) 覚え方! 「身の上に心配あるさ〜♪」 (3の上に4πrさ〜♪) 問題 球の半径が3cmのとき、体積を求めなさい。 こちらも代入しておしまいです☆



球欠と球冠 Fukusukeの数学めも



球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear
円形度 circularity (等面積円の円周)/(周長) 球の表面積 \(\pi D^2\) 球の体積 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3\) 球の質量 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3 \rho\) 球の体積基準比表面積(単位体積当たりの表面積)数学 何度もすみません。 今度は「球体の面積の求め方」を知りたくなりました。 (学校で使うので) 誰でも良いので、よろしくお願いします。


Object 01



ガウスの法則とは 公式 や 積分形 や 微分形 などを解説


球の体積と表面積を積分で証明 高校数学の美しい物語



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su


1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



球の表面積の公式について みたにっき はてな



球の体積と表面積 Youtube



球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



数学1年空間図形 中学数学に関する質問 勉強質問サイト



球の体積と表面積 公式と計算問題と証明 Irohabook


微分でつなげる円や球の公式 すうがくブログ 式変形ch
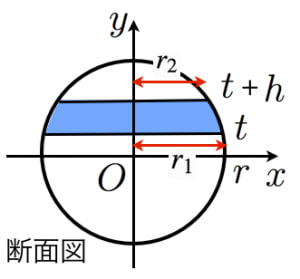


球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語



中学2年 図形 中学数学に関する質問 勉強質問サイト



球面三角形の面積の求め方 理数アラカルト


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球体の表面積 積分で求める方法 うちーノート



球の表面積 体積 身勝手な主張



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の表面積と体積の公式 数学fun


球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ


球の表面積の公式の求め方


学校で球の面積の求め方を 3分の2すると言われたのですが 調べ Yahoo 知恵袋



楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
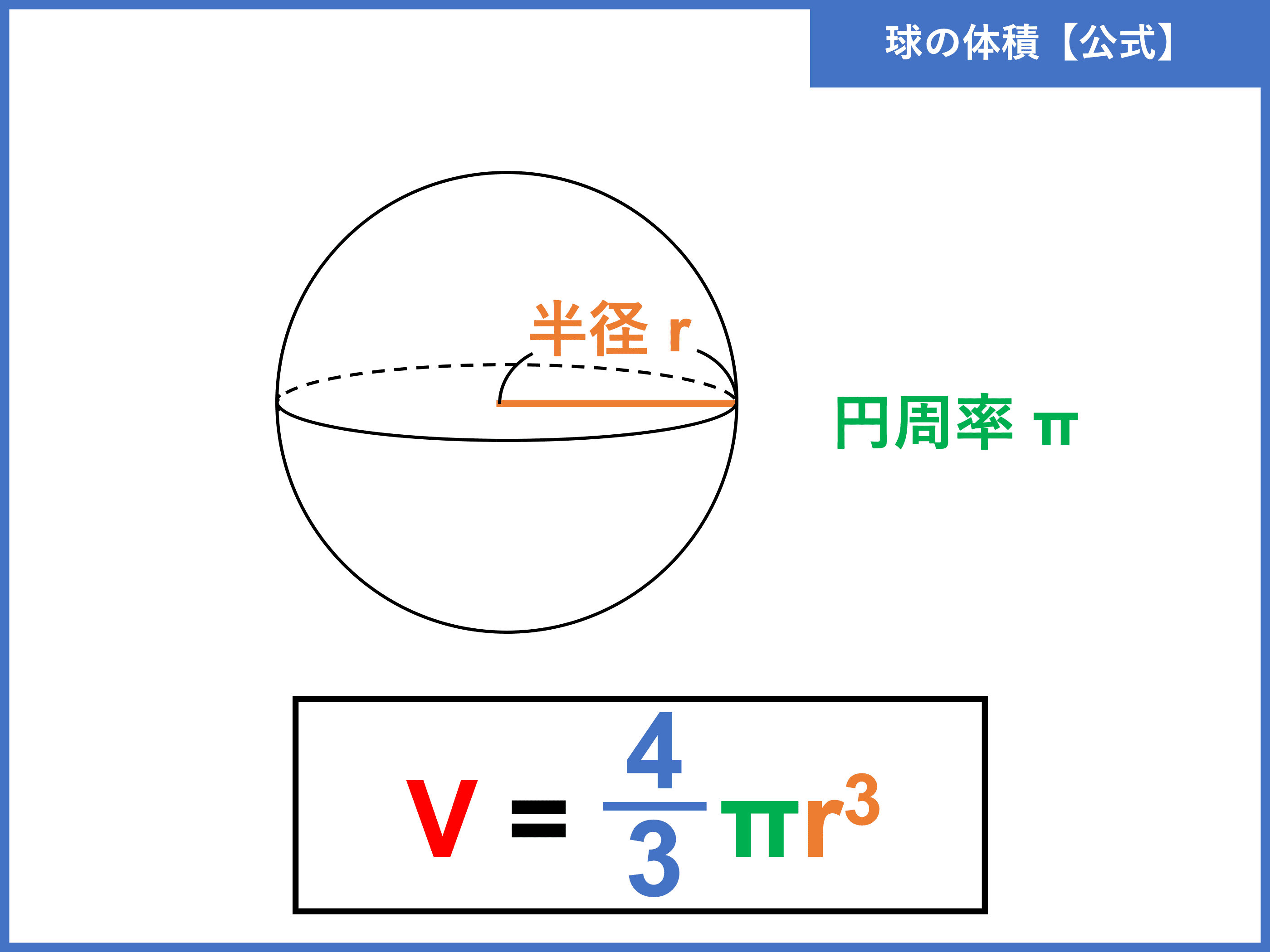


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


半径3cmの球の表面積 体積の求め方を教えて下さい Yahoo 知恵袋



球の表面積と体積の公式 数学fun



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ


水平投影面積とは 1分でわかる意味 計算法 法面


数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



表面積の求め方 計算公式一覧



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



球の表面積の求め方 その3 感じる科学 味わう数学


球の問題 苦手な数学を簡単に


球の体積と表面積を積分で証明 高校数学の美しい物語



中1 数学 6 5 球の体積 表面積 Youtube



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



勉強しよう数学 球の表面積を積分で求める



球の表面積の公式について みたにっき はてな



円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積を重積分を使って計算してみた Youtube


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト



中1 数学 中1 84 球について Youtube


半球の体積と表面積を計算する 具体例で学ぶ数学
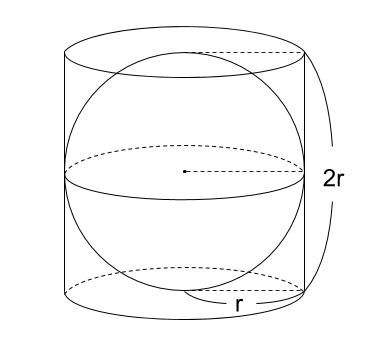


中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
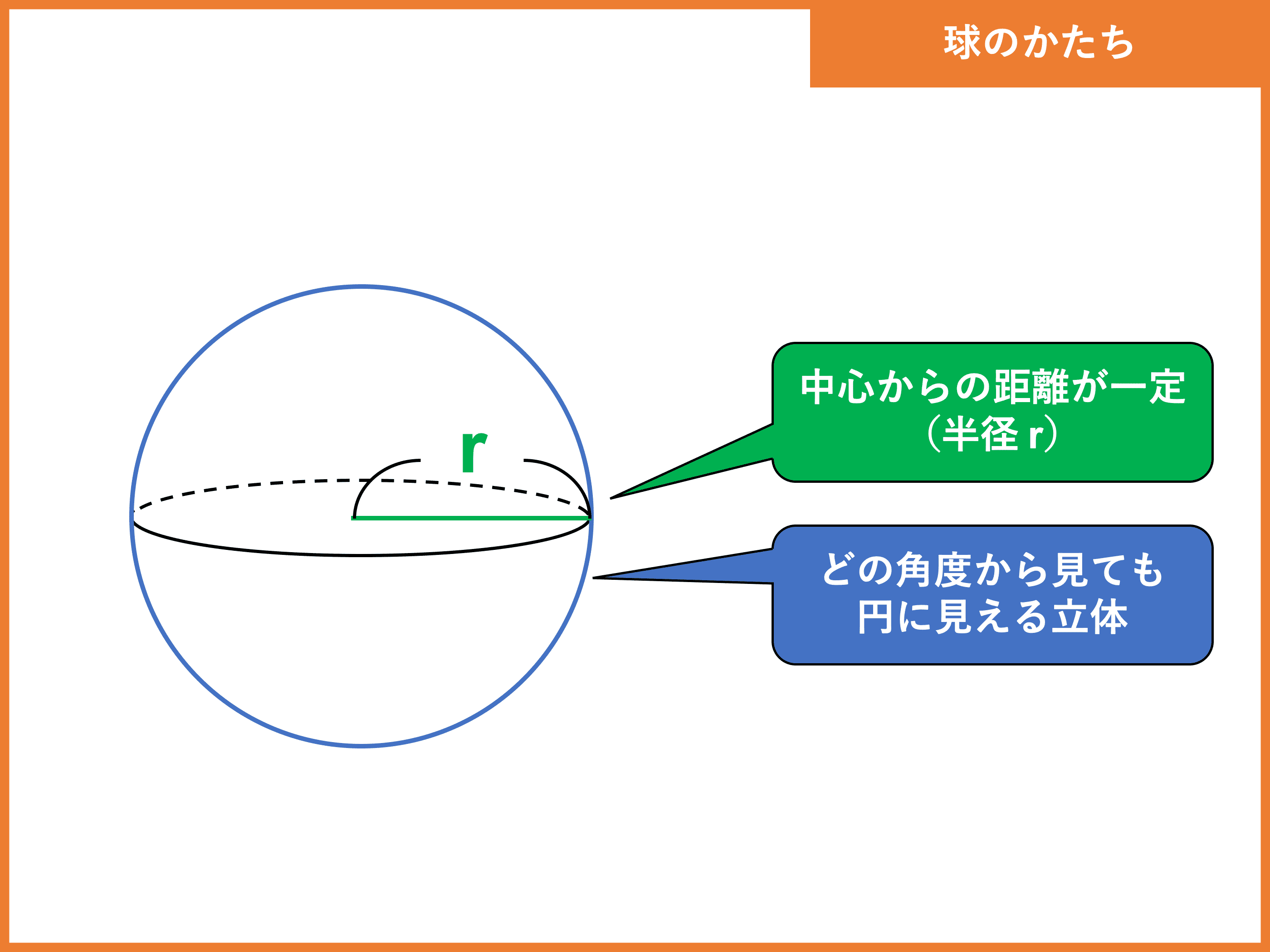


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球体を切った時の直径の求め方 球体を切った時の直径の求め方を教えて 数学 教えて Goo


球帯と球冠


Math 円柱 内接する球 円錐の体積と表面積 働きアリ
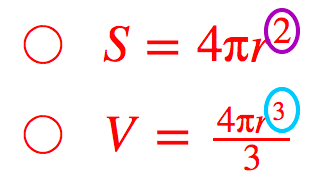


球の表面積と体積の求め方 苦手な数学を簡単に
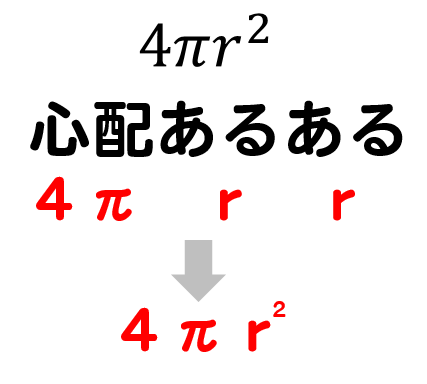


球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
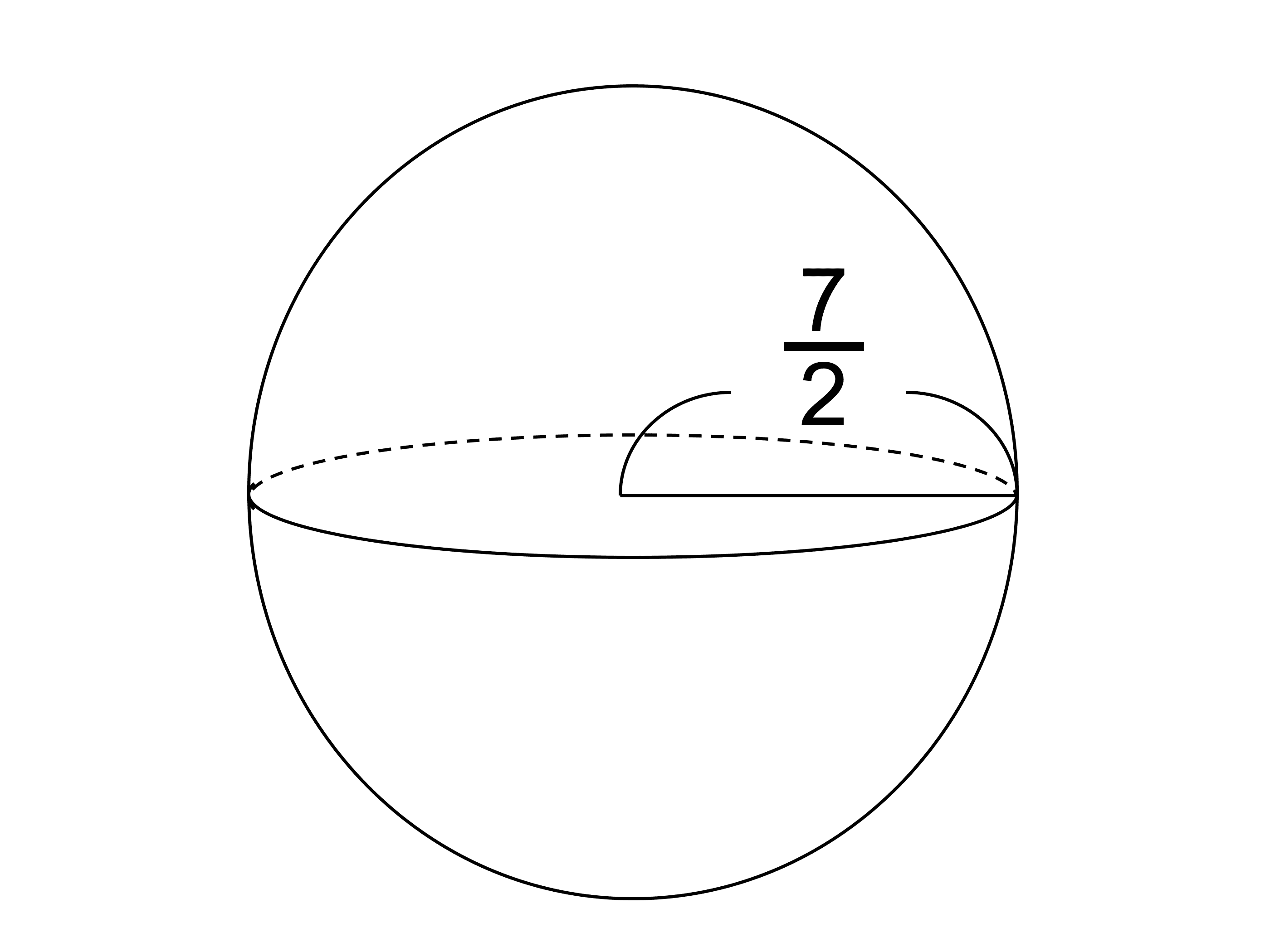


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


球の表面積の公式の求め方



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
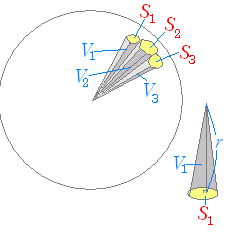


例題対比 球の体積と表面積



中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球の体積公式の微分が表面積になっている理由 Youtube


Sphere 01



Mathematics 球の体積と表面積を求める公式 働きアリ
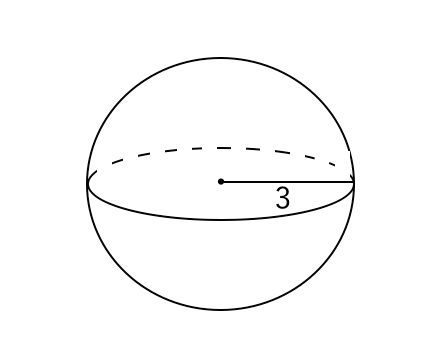


球の表面積と体積の求め方 苦手な数学を簡単に



初等幾何 球の表面積を求める 大人が学び直す数学
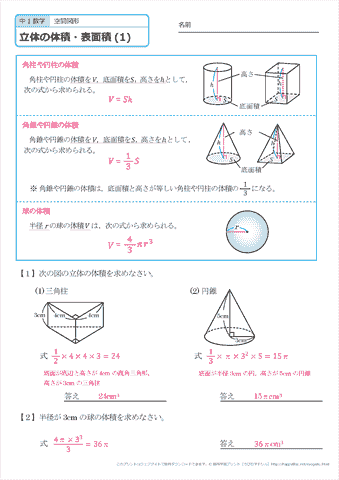


中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館
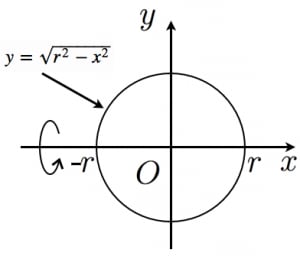


球の体積と表面積を積分で証明 高校数学の美しい物語


Sphere 01



球の体積 表面積 無料で使える中学学習プリント



中一数学 球の表面積と体積 中学生 数学のノート Clear


大学入試問題



球の表面積と体積の公式 数学fun



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
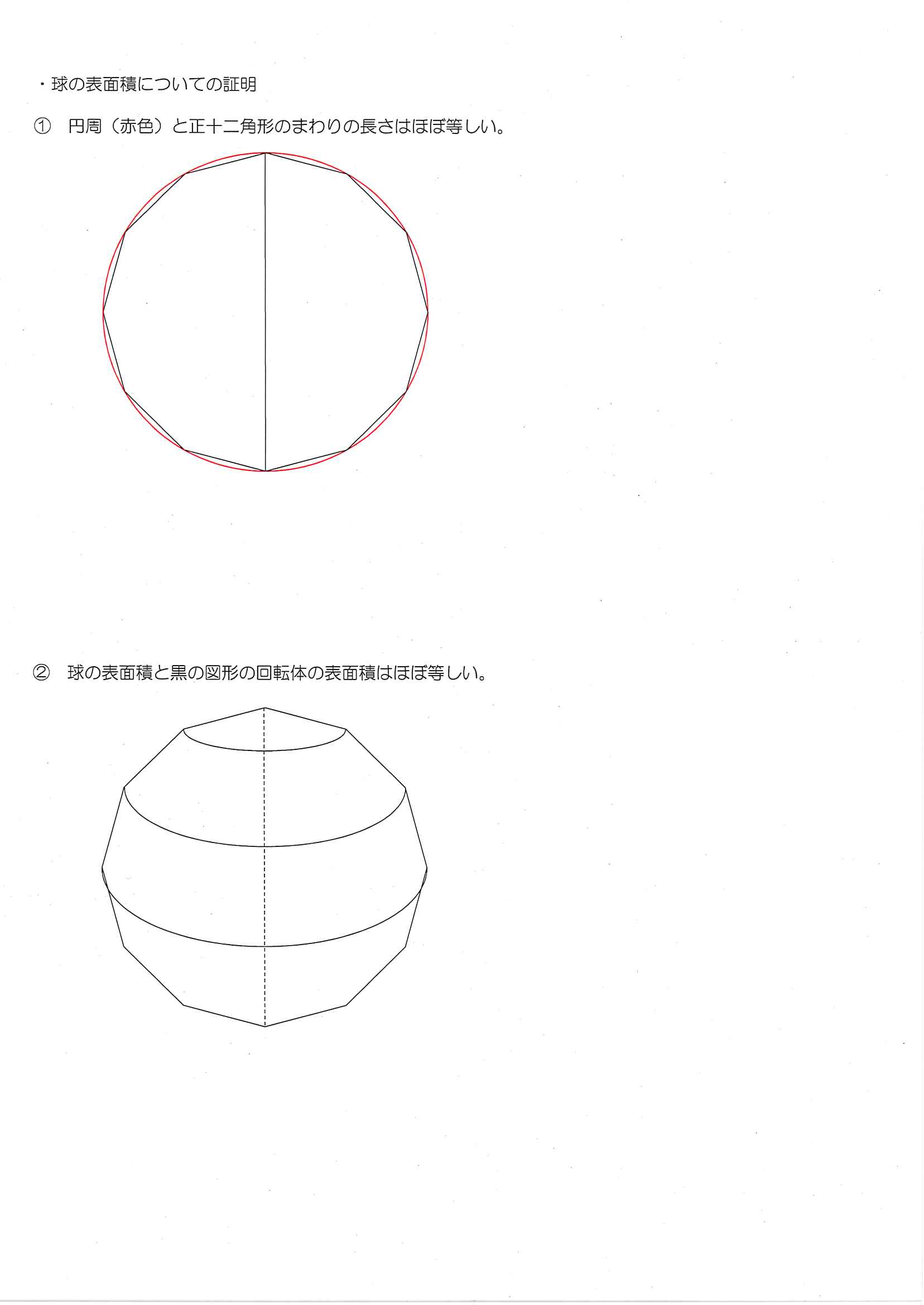


優雅 球体 表面積 求め 方 壁紙 配布



球の表面積と体積の公式 数学fun
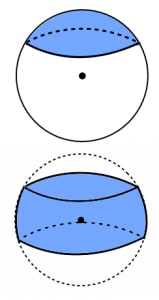


球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語
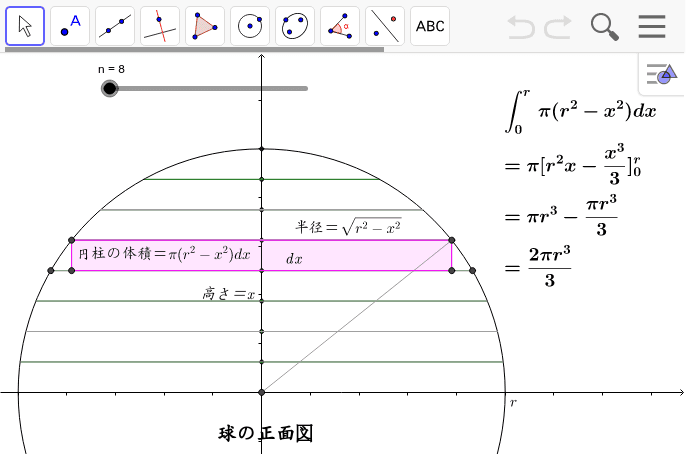


球の体積の積分 Geogebra



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



角錐 円錐の体積と表面積の公式 数学fun


